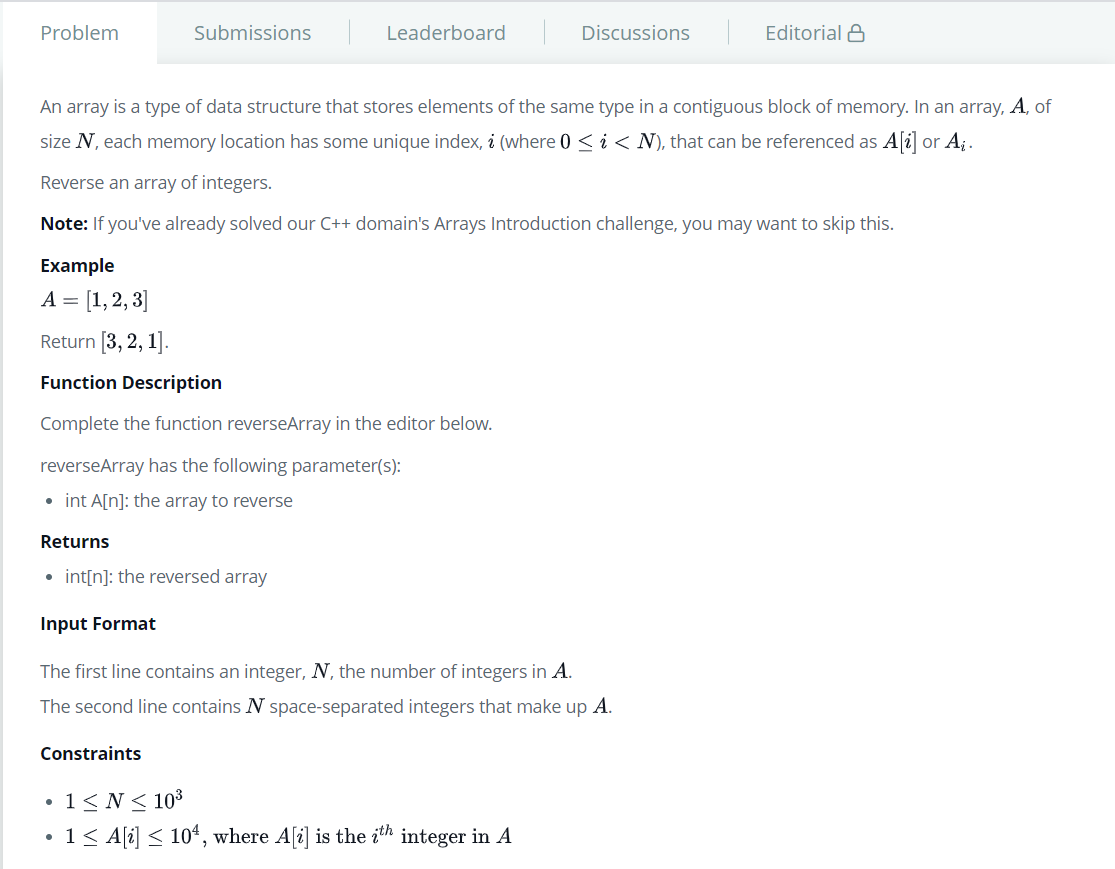
# Array - DS (array)
[문제]

[코드]
int* reverseArray(int a_count, int* a, int* result_count) {
int temp;
*result_count=a_count;
a_count--;
for(int i = 0; i <= a_count/2; i++){
temp=a[i];
a[i]=a[a_count-i];
a[a_count-i]=temp;
}
return a;
}
[코드설명]
temp: 배열의 값을 옮길 때 임시로 저장할 변수
result_count에 a_count 값을 미리 옮겨 놓고, a_count에 마지막 값의 인덱스를 저장하기 위해 a_count를 1감소시켰다.
(a[0], a[n-1]), (a[1], a[n-2]), ...순서쌍의 값이 서로 바뀌도록 하기 위해 for문이 i가 0부터 a_count/2으로 증가될 때까지 반복한다(인덱스의 중간값까지).
temp에 a[i]의 값을 저장해가면서 a[i]와 a[a_count-i]의 값을 서로 바꾼다.
for문 종료 후에 포인터 a를 반환한다.
[채점 결과]

# Equal Stacks (stack)
[문제]

[코드]
int sum(int* arr, int count)
{
int sum = 0;
for(int i = 0; i < count; i++)
sum += arr[i];
return sum;
}
int min_h(int n1, int n2, int n3)
{
int min = n1;
min = min < n2 ? min : n2;
min = min < n3 ? min : n3;
return min;
}
void reverse(int* h, int n)
{
int temp;
n--;
for(int i = 0; i <= n/2; i++){
temp = h[i];
h[i] = h[n-i];
h[n-i] = temp;
}
}
int equalStacks(int h1_count, int* h1, int h2_count, int* h2, int h3_count, int* h3) {
int n1 = 0, n2 = 0, n3 = 0;
int min;
n1 = sum(h1, h1_count);
n2 = sum(h2, h2_count);
n3 = sum(h3, h3_count);
min = min_h(n1, n2, n3);
reverse(h1, h1_count);
reverse(h2, h2_count);
reverse(h3, h3_count);
while(!(n1==n2&&n2==n3))
{
if(n1 > min)
n1 -= h1[h1_count-1], h1_count--;
if(n2 > min)
n2 -= h2[h2_count-1], h2_count--;
if(n3 > min)
n3 -= h3[h3_count-1], h3_count--;
min = min_h(n1, n2, n3);
}
return min;
}[코드설명]
① sum()
sum: 배열 원소의 합
i가 0부터 count-1까지 증가하면서 arr[i]의 값을 sum에 더한다.sum을 반환한다.
② min_h()
min: 세 가지 스택의 sum중 제일 작은 수
n1, n2, n3: 세 가지 스택의 sum
min과 스택의 sum을 비교해서 더 작은 수를 min에 저장한다.
min을 반환한다.
③ reverse()
위쪽의 Array - DS에서 구현한 reverseArray()와 동일한 알고리즘이다.
for문에서 i가 0부터 배열 인덱스의 중간까지 증가하면서 h[i]와 h[n-i]의 값이 서로 바뀐다.
④ equalStacks()
min: 세 가지 스택의 sum중 제일 작은 수
n1, n2, n3: 세 가지 스택의 sum
sum()로 세 스택의 sum을 구하고, 그 중 제일 작은 수를 min에 저장한다.
/* 필자가 문제를 제대로 이해하지 못한건지, 제일 먼저 push된 수가 먼저 pop되는 것 같이 보였다. stack을 제대로 구현하기 위해서 min을 구하기에 앞서 각 스택의 값을 reverse했다. */
reverse()로 세 스택의 값을 거꾸로 재배치했다.
min과 각 스택의 sum을 비교해서 스택의 sum이 더 크면 sum에서 스택의 마지막 값을 빼고, 인덱스를 감소시킨다.위의 명령을 완료하면 바뀐 각 스택의 sum에 대해서 다시 min을 구한다.이 과정을 n1, n2, n3이 같을 때까지 반복한다.n1=n2=n3이면 min을 반환한다.
[채점 결과]

'알고리즘' 카테고리의 다른 글
| [HackerRank] Print the Elements of a Linked List / Insert a Node at the Tail of a Linked List (0) | 2021.04.11 |
|---|---|
| [HackerRank] 2D Array - DS / Intro to Tutorial Challenges (0) | 2021.04.01 |
| [BOJ] 13235/2908 (0) | 2021.02.22 |
| [BOJ] 4673/16503 (0) | 2021.02.17 |
| [BOJ] 1316/2869 (0) | 2021.02.07 |