# QHEAP1 (Heap)
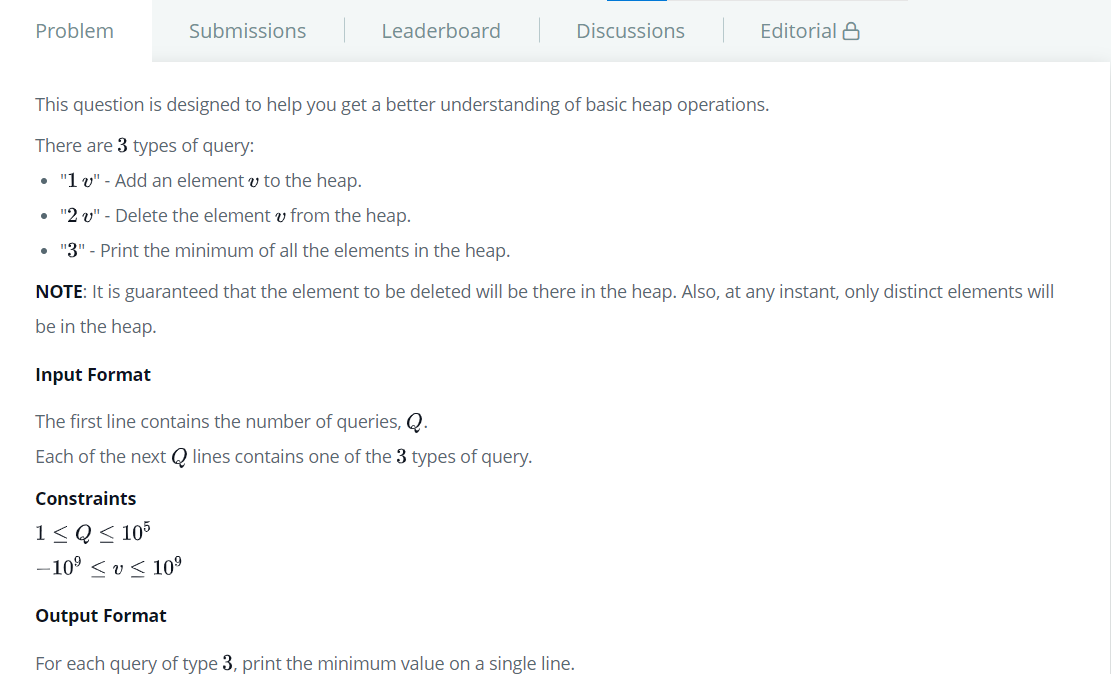
[문제]

[코드]
#include <stdio.h>
#include <string.h>
#include <math.h>
#include <stdlib.h>
typedef struct {
int *arr;
int total_node;
} Heap;
void init_heap(Heap * heap, int n) {
heap->arr = (int*)malloc(sizeof(int) * (n + 1));
heap->total_node = 0;
}
void insert_heap(Heap *heap, int data)
{
int i;
i = ++(heap->total_node);
while ((i != 1) && (data < heap->arr[i / 2]))
{
heap->arr[i] = heap->arr[i / 2];
i /= 2;
}
heap->arr[i] = data;
}
void delete_heap(Heap *heap, int search) {
int i;
for (i = 1; i <= heap->total_node; i++) {
if (heap->arr[i] == search)
break;
}
if (i > heap->total_node) return;
int child = i * 2;
int temp = heap->arr[heap->total_node--];
while ((temp > heap->arr[child]) && (child <= heap->total_node) && (child + 1 <= heap->total_node))
{
if (heap->arr[child] < heap->arr[child + 1])
{
heap->arr[child / 2] = heap->arr[child];
child *= 2;
}
else
{
heap->arr[child / 2] = heap->arr[child + 1];
child = (child + 1) * 2;
}
}
if ((child + 1 <= heap->total_node) && temp > heap->arr[child + 1])
{
heap->arr[child / 2] = heap->arr[child + 1];
child = (child + 1) * 2;
}
else if ((child <= heap->total_node) && (temp > heap->arr[child]))
{
heap->arr[child / 2] = heap->arr[child];
child *= 2;
}
heap->arr[child / 2] = temp;
}
int main() {
int N, type, data;
Heap heap;
scanf("%d", &N);
init_heap(&heap, N);
for (int i = 0; i < N; i++) {
scanf("%d", &type);
switch (type) {
case 1:
scanf("%d", &data);
insert_heap(&heap, data);
break;
case 2:
scanf("%d", &data);
delete_heap(&heap, data);
break;
case 3:
printf("%d\n", heap.arr[1]);
break;
}
}
return 0;
}
[코드설명]
MinHeap Tree를 구조체로 정의 → Heap으로 typedef.
init_heap 함수에서 arr에 sizeof(int)*(n+1)크기의 메모리 할당, 전체 노드 수 0으로 초기화.
insert_heap 함수에서 새로 추가할 노드의 위치가 1이면 원래 empty heap이었다는 의미이므로 heap->arr[1]에 data 저장.
(트리에서 부모와 자식간의 관계를 식으로 표현하기 위해 인덱스 1부터 시작함)
empty heap이 아니면 부모 노드의 data 값과 대소 비교해서 더 작은 값을 부모 노드에 위치시킴.
delete_heap 함수에서 삭제할 노드의 인덱스를 찾아 i에 저장. 트리에 삭제하고자 하는 값이 없으면 함수 종료.
삭제할 노드의 left 노드 위치를 child에 저장. 삭제된 공간을 채우기 위해 트리의 맨 마지막 값을 temp에 저장.
현재 left와 right 노드가 모두 존재할 경우, temp와 left, right 노드에서 제일 작은 값을 찾아 위치 변경.
while문을 나왔을 때 발생할 수 있는 경우는
① 현 위치에서 left와 right노드가 존재하고, temp가 left노드 값 보다 더 작은 경우
② left노드만 존재하는 경우
③ 자식 노드가 없는 경우
이렇게 3가지로 나눌 수 있다.
각각의 경우를 if-else if문의 조건으로 표현.
(3번째 같은 경우는 while문을 나오자마자 맨아래 코드를 적용하면 되므로 if-else if 조건에 포함시키지 않음)
위 함수들을 기반으로 main 함수에서 switch문으로 각각의 쿼리를 처리한다.
[채점 결과]

# Quicksort 1 - Partition (Sorting)
[문제]


[코드]
int* quickSort(int arr_count, int* arr, int* result_count) {
int pivot = arr[0], i = 0, j = arr_count-1;
int *brr = (int*)malloc(sizeof(int)*arr_count);
for(int k = 1; k < arr_count; k++)
{
if(pivot > arr[k])
brr[i++] = arr[k];
else
brr[j--] = arr[k];
}
brr[i] = pivot;
for(int k = 0; k < arr_count; k++)
arr[k] = brr[k];
*result_count = arr_count;
return arr;
}
[코드설명]
추가 배열을 사용해서 해결.
arr[0]을 pivot(기준수)으로 설정.
추가 배열 brr을 동적할당 받음.
brr배열에 pivot보다 작은 수는 왼쪽, 큰 수는 오른쪽으로 정렬.
모든 원소에 대해 정렬이 끝나면 마지막에 pivot 추가.
arr에 brr의 값을 복사.
[채점 결과]

'알고리즘' 카테고리의 다른 글
| [HackerRank] Left Rotation / Dynamic Array (0) | 2021.07.14 |
|---|---|
| [HackerRank] Jesse and Cookies / Insertion Sort - Part 1 (0) | 2021.07.09 |
| [HackerRank] Tree: Level Order Traversal / Binary Search Tree : Insertion (0) | 2021.06.26 |
| [HankerRank] Tree: Postorder Traversal / Maximum Element (0) | 2021.05.28 |
| [HackerRank] Tree: Height of a Binary Tree / Tree: Inorder Traversal (0) | 2021.05.20 |