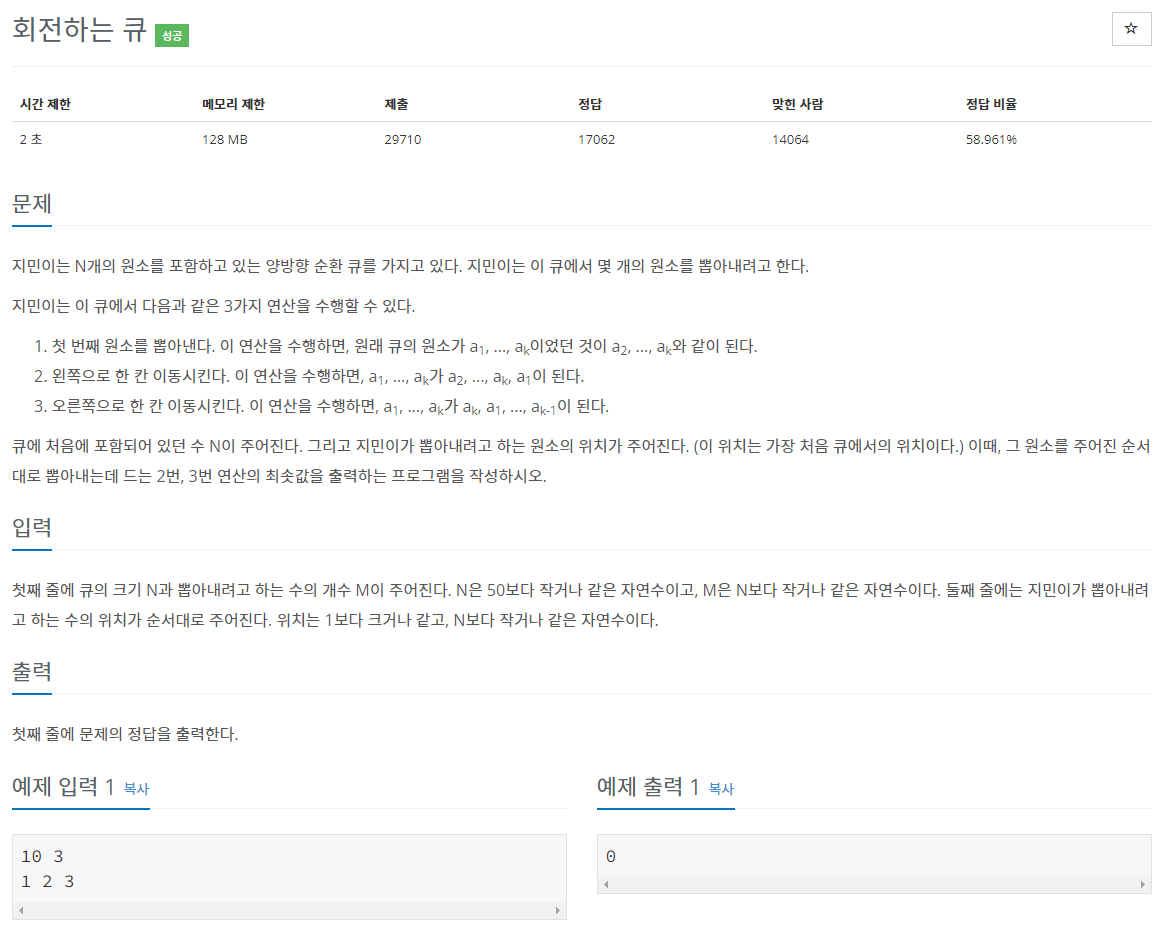
문제: https://www.acmicpc.net/problem/1021

#include <bits/stdc++.h>
using namespace std;
deque<int> dq;
int n, m;
int idx[50];
int num, dq_size;
int result;
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cin >> n >> m;
for (int i = 0; i < m; i++) cin >> idx[i];
for (int i = 1; i <= n; i++) dq.push_back(i);
for (int i = 0; i < m; i++) {
int k;
for (k = 0; k < dq.size(); k++)
if (dq[k] == idx[i]) break;
dq_size = dq.size();
if (k < dq_size - k) {
result += k;
while (k--) {
num = dq.front();
dq.pop_front();
dq.push_back(num);
}
} else {
k = dq_size - k;
result += k;
while (k--) {
num = dq.back();
dq.pop_back();
dq.push_front(num);
}
}
dq.pop_front();
}
cout << result << '\n';
}문제 이름을 보고 처음엔 순환큐를 이용해서 풀어야 한다고 생각했다.
그러나 문제를 자세히 본 후에는 생각이 조금 바뀌었다.
문제에서 수행할 수 있는 연산은 딱 3가지다.
1. 첫 번째 원소를 뽑아내기
2. 모든 원소를 왼쪽으로 한 칸 이동하기
3. 모든 원소를 오른쪽으로 한 칸 이동하기
여기서 원소를 이동하는 연산을 잘 생각해보자.
2번 연산을 수행하면 a1, a2, a3, ..., ak => a2, a3, a4, ..., ak, a1이 되고,
3번 연산을 수행하면 a1, a2, a3, ..., ak => ak, a1, a2, ..., ak-1이 된다.
각 연산을 단순하게 생각해보면 2번 연산은 front를 pop하고 back에 push한 것이고,
3번 연산은 back을 pop하고 front에 push한 것이다.
즉 dequeue(덱)을 사용해서 문제를 해결할 수 있는 것이다.
가장 먼저 원소의 index를 담은 큐를 만들었다. => dq
해당 큐를 만든 이유는 pop연산을 한 이후에도 맨처음 큐에서의 원소의 위치를 기억하기 위해서다.
해당 큐는 1부터 입력으로 주어진 n까지의 수가 들어있다.
이젠 입력으로 받은 m만큼 연산의 최솟값을 구해야 한다.
k는 큐에서 제거하고자 하는 원소의 인덱스다.
idx 배열은 입력으로 받은 큐에서 제거해야 하는 원소의 위치다. => 해당 값은 가장 처음의 큐의 위치
인덱스는 현재 원소의 앞에 있는 원소의 개수와 같기 때문에 k만큼 왼쪽으로 이동하면 제일 첫 번째 원소가 될 수 있다.
반대로 큐의 원소의 개수에서 인덱스를 뺀 값만큼 오른쪽으로 이동하면 마찬가지로 현재 원소가 제일 첫 번째 원소가 될 수 있다.
이 원리를 이용해서 k에 현재 내가 제거하고자 하는 원소의 인덱스를 구한다.
dq[k]와 index[i]를 비교하면 내가 제거하고자 하는 원소의 인덱스를 구할 수 있다.
이제 k와 dq_size - k를 비교해서 어느 값이 더 작은지 찾아야 한다.
더 작은 쪽이 연산의 개수를 줄일 수 있는 방법이기 때문이다.
k가 더 작다면 제거 대상이 앞쪽이 있다는 의미이므로 front의 값을 back으로 옮기는 연산을 하고,
그 반대라면 제거 대상이 뒤쪽에 있다는 의미이므로 back의 값을 front로 옮기는 연산을 하면 된다.
이때마다 연산의 개수는 result에 더해주면 연산의 최솟값을 구할 수 있다.

'알고리즘' 카테고리의 다른 글
| [BOJ] 3986: 좋은 단어 (0) | 2022.10.01 |
|---|---|
| [BOJ] 5430: AC (0) | 2022.10.01 |
| [BOJ] 4949: 균형잡힌 세상 (0) | 2022.09.30 |
| [BOJ] 10886: 덱 (0) | 2022.09.29 |
| [BOJ] 2164: 카드2 (0) | 2022.09.29 |