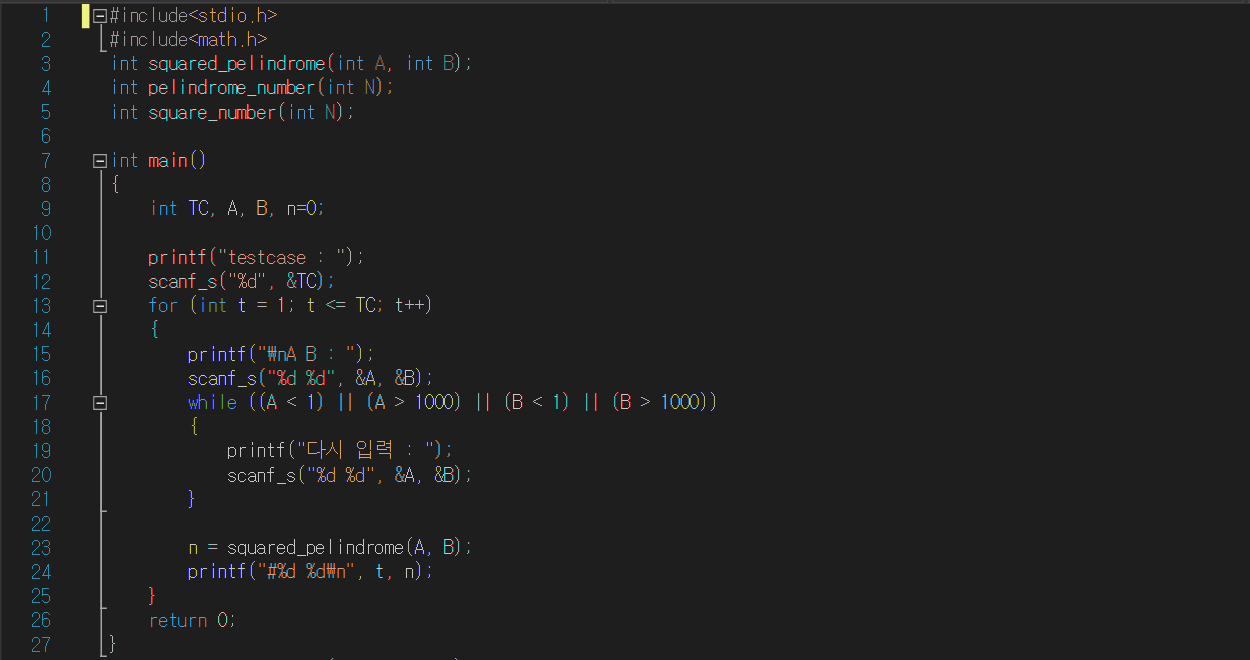
#10570 : 제곱 팰린드롬 수
[코드]

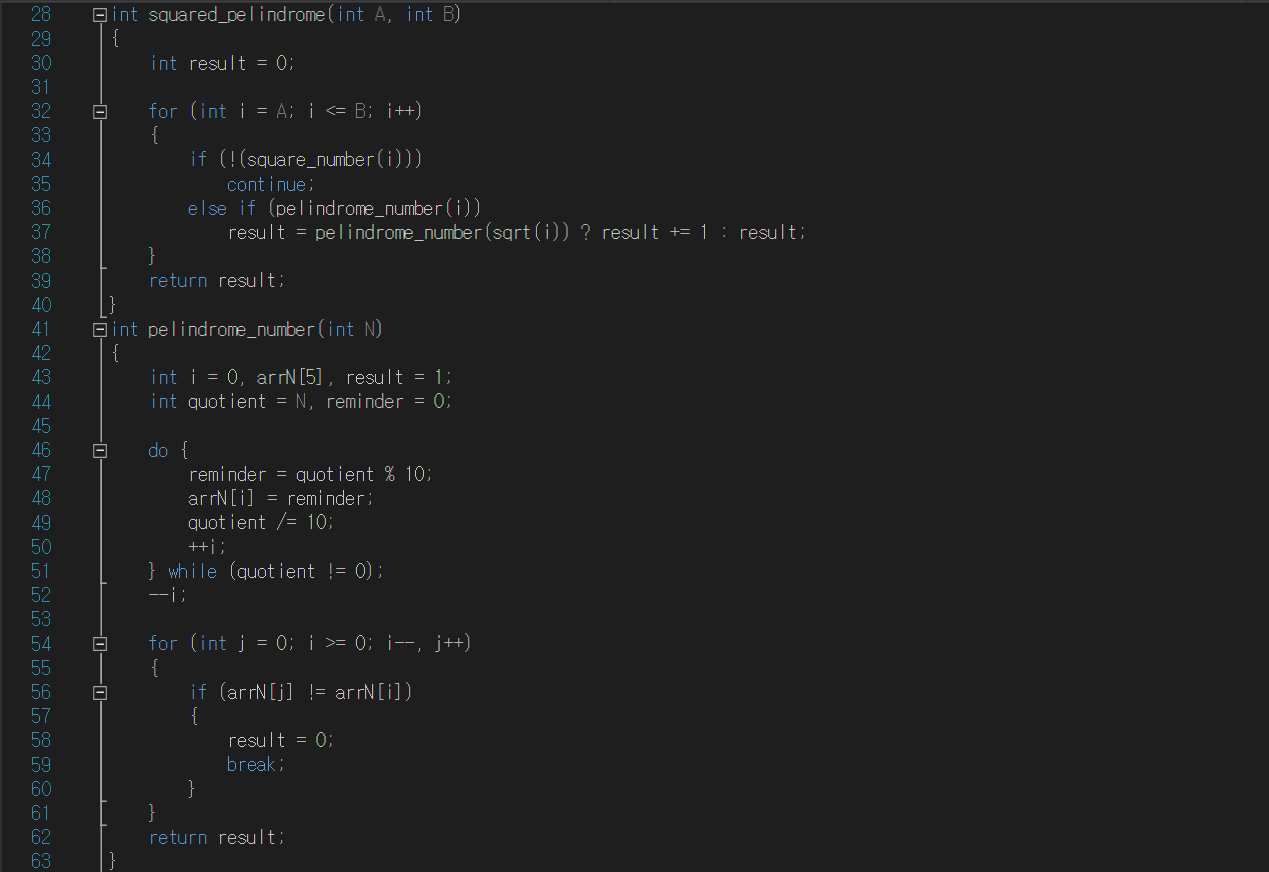

[코드설명]
① main
A와 B를 입력 받고, 1<=(A, B)<=1000가 아니면 while문으로 A와 B가 1이상 1000이하가 될 때까지 입력 받는다. squared_pelindrome함수에 A, B를 인자로 전달하면 n에 제곱 팰린드롬 수를 리턴한다.
② squared_pelindrome
main함수에서 A와 B를 인자로 받는다. for문으로 i를 A부터 B까지 증가시켜 A와 B사이의 모든 수를 검사한다. 제곱 팰린드롬 수는 제곱근도 팰린드롬 수여야 하기 때문에 i가 제곱수가 아니면 제곱 팰린드롬 수가 아니다. 따라서 if문에서 i가 제곱수가 아니면 현재 반복을 건너뛴다. i가 제곱수이면 else if문에서 pelindrome_number함수로 i가 팰린드롬 수인지 아닌지 확인한다. 참이면 i의 제곱근도 pelindrome_number함수로 팰린드롬 수인지 아닌지 확인한다. 이때 pelindrome_number(sqrt(i))가 참이면 result가 1증가하고, 거짓이면 값의 변동이 없다.
③ pelindrome_number
팰린드롬 수인지 확인하기 위한 변수를 인자로 받는다. N의 회문검사를 하기 위해 N을 10으로 나눈 나머지를 arrN배열에 저장하는 수행을 반복해서 arrN배열에 N의 숫자열을 반대로 담았다. 코드를 보면 반복문으로 몫을 계속 나눠야 하기 때문에 quotient에 N을 대입하고 시작했다. do에서 quotient를 10으로 나눈 나머지를 reminder에 저장하고, arrN[i]에 reminder를 저장했다. 그리고 quotient/10 몫을 quotient에 저장하고, 다음 반복을 위해서 arrN배열의 인덱스 값이 i를 1증가 시켰다. 그러면 while에서 quotient값을 확인하고 0이 아니라면 다음 반복에서 quotient값으로 같은 동작을 수행한다. do while문이 끝나면 i가 arrN배열에 실제로 값이 들어있는 인덱스보다 1이 많기 때문에 1을 빼준다. 그리고 for문에서 j를 0부터 시작하고, i는 0이 될 때까지 1씩 줄여가면서 arrN배열의 값을 비교하도록 했다. 만약 arrN[j]과 arrN[i]이 다르다면 result에 0을 대입하고 반복문을 빠져나온다. 여기서 result가 1이면 N은 팰린드롬 수이고, 0이면 팰린드롬 수가 아니다.
④ square_number
square_pelindrome함수에서 검사하는 수가 제곱수인지 확인할 때 사용한다. sqrt함수를 사용해서 N의 제곱근을 root_n에 구하고, root_n을 int로 캐스팅한 값을 n에 저장했다.(sqrt함수는 double자료형을 반환) 그 후 if문으로 n과 root_n을 비교해서 값이 다르면 result에 0을 대입한다. 여기서 result가 1이면 N은 제곱수이고, 0이면 제곱수가 아니다.
[실행결과]

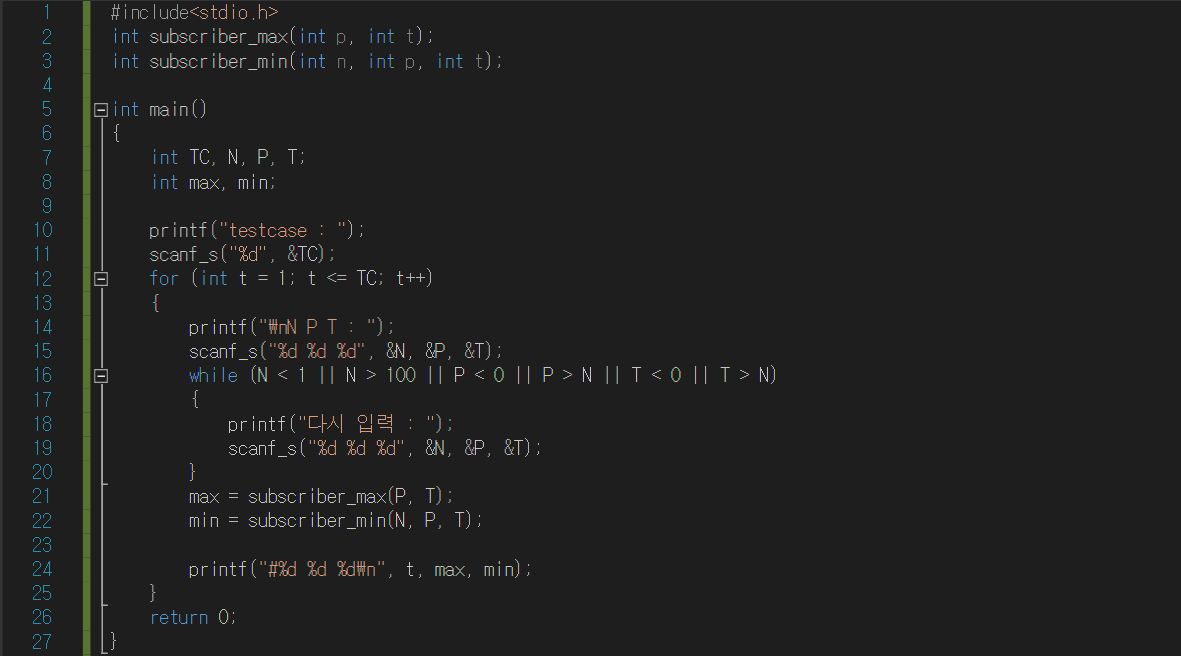
# 10200 : 구독자 전쟁
[코드]
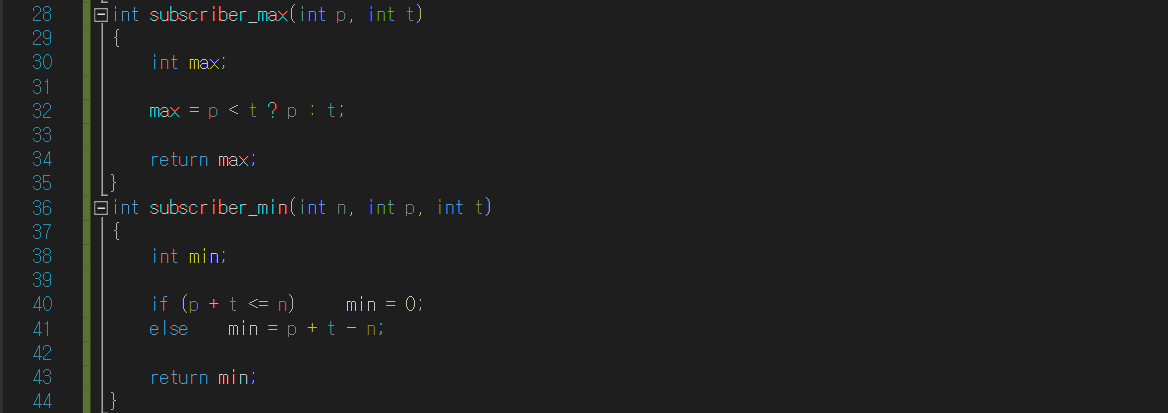
[코드설명]
① main
전체 사람 수 N, P채널 구독자 수 P, T채널 구독자 수 T를 조건에 맞게 입력 받는다. subscriber_max 함수와 subscriber_min 함수로 두 채널 모두 구독한 구독자 수의 최대와 최소를 구한다.
② subscriber_max
두 채널 모두 구독한 구독자의 최대값은 P채널 구독자와 T채널 구독자 중 더 작은 값에 해당한다. 따라서 main으로 부터 P채널 구독자와 T채널 구독자 값을 가져오고, 조건 연산자를 사용해서 p와 t중 더 작은 값을 max에 저장한다. p와 t가 같은 경우에는 t의 값이 max에 저장되지만 둘 다 같은 값이므로 상관하지 않는다.
③ subscriber_min
두 채널 모두 구독한 구독자 수가 최소이려면 한 사람이 최대한 한 채널만 구독하도록 해야 한다. P채널과 T채널을 구독한 구독자 수를 합하고 이를 N보다 큰지 작은지를 따진다. 만약 N보다 작다거나 같다면 모든 사람이 두 채널을 동시에 구독할 수 없게 배치할 수 있다. 따라서 이 경우는 min이 0이 된다. 만약 N보다 크다면 P채널 구독자와 T채널 구독자 수를 합한 다음 N을 빼야한다. p+t-n에서 남은 값만큼 두 채널을 동시에 구독한 구독자 수가 있다는 뜻이므로 이 경우 min은 p+t-n이다.
[실행결과]

'알고리즘' 카테고리의 다른 글
| [SWEA] 10726/8931 (0) | 2020.10.02 |
|---|---|
| [SWEA] 9940/10032 (0) | 2020.09.24 |
| C정리 3주차 (0) | 2020.07.11 |
| C정리 2주차 (0) | 2020.07.11 |
| C정리 1주차 (0) | 2020.07.06 |